One of the Key Word about Interfaces today is Responsive Design: For a Mobile App, interfaces not only have to be the simplest possible, they have to be clear, and they have to propose only awaited functionalities that users will understand: they had to be adaptative.
So not surprisingly, Math Touch Book displays nothing else than what you wrote on the screen. Then touching a Math expression unfolds a Menu that proposes a short list of features according to that expression.

Adaptative Menus are not new, but here, the program must “think” to guess the list of functionalities, operations, modifiers: Expressions can be developed or not, Simplified or not, resolved or not. And notice, some of those features can take multiple passes, like Equation resolutions.
It might surprise you, but a bit of Artificial Intelligence (AI) intervenes at this level: The same basic AI algorithm is used, both to select the menu entries and to resolve equations.
With the advent of multi-threaded mobile CPU and GPUs this last decade, Robotics and Artificial intelligence are subject to permanent breakthrough. On the software side the AI subject becomes bigger every day. But large industrial AI programs for robots, that have to compute an impressive sum of data, and more little algorithms managing equations (like MathTouch Book does) have things in common: they both manage their objects using Graph Theory, and they both create and test algorithms before applying them for real.
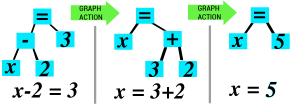
Let’s have a look at what Math Touch Book does when it resolves an equation:
First, Equations are defined by Graph Trees, where the root element is an equal sign.
Elements in a tree are all attached to another. That’s what Graph Theory is about and we, computer scientists, usually think it’s a nice way to manage data.
A good Graph theory framework should also have methods for cloning graphs, detaching branches of the tree, re-attach them elsewhere, and the ability to use one or another element allocators, amongst other things.
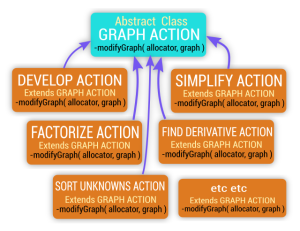
Then we have some bricks here, that represents schematically classes available in the program, it’s a “Object Oriented” concept. This scheme tells us each of these classes are “GraphActions”, and each is able to modify a graph in their own way. They are available to be used by the Artificial Intelligence.
So now that we know the shape of the data, the tools to modify it, we want the program to find itself a way to resolve the equation. How ?
An equation resolution algorithm can be expressed as a list of “GraphActions”. But what GraphActions to use, in what order ?
And what happens if the program find a wrong algorithm ? the graph would be destroyed !
No, because we can clone the graph and test modifications on the clone.
we can also simply look at the shape of a graph, and decide to modify it in a way or another according to its shape. (You now understand the usefulness of having clone functions and special allocators in your graph framework.)
Written in pseudo-code, you can find a resolution algorithm like this:
class changeThisShapeAction extends GraphAction
class changeTHATShapeAction extends GraphAction
...
get_Action_List_For_Resolution( listOfActions , equationGraph )
{
tempGraphAllocator // init an allocator to experiement
// create a temporary clone to experiment
cloneOfEquation = equationGraph.clone(tempGraphAllocator)
// this loop search a shape that can be resolved
while( cloneOfEquation has no resolvable shape )
{
if(cloneOfEquation has "this" shape)
{
didSomething = changeThisShapeAction.
modifyGraph(tempGraphAllocator,cloneOfEquation);
if(didSomething) listOfActions.add(changeThisShapeAction)
}
if(cloneOfEquation has THAT shape)
{
didSomething = changeTHATShapeAction.
modifyGraph(tempGraphAllocator,cloneOfEquation);
if(didSomething) listOfActions.add(changeTHATShapeAction)
}
(... here are a lots of modifier actions to test accordingly)
} // end of loop
// here equation could be resolvable or not :
if(cloneOfEquation first degree) listOfActions.add(finaliseFirstDegree)
if(cloneOfEquation is quadratic) listOfActions.add(finaliseQuadratic)
if(cloneOfEquation not resolvable) listOfActions.add(finaliseNoSolution)
// the magic here, is we just cancel everything done on the tempGraph...
tempGraphAllocator.free()
// We return the exact list of modifiers that finds the solution.
return listOfActions
}
Acting innocently, with just one accumulator list, a loop and an object oriented set of classes, we have here an algorithm that … creates an algorithm. and it works !
The human brain actually does more or less this “imagine what is the most interesting thing to do, and then do it” game. The temporary allocated memory can be seen as a short-lived “imagination”. Obviously the real code is a little bigger, but the main idea is here.
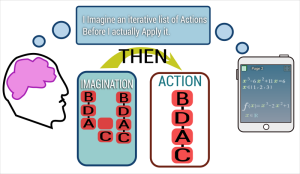
To me, the greatest of all things is that, at this level, the algorithm is found, it is available for use, but you can or cannot use it inside the application; it’s up to the user, he may use another modifier, and in some way this “search what to do” Artificial Intelligence algorithm can also be seen as a recursive extension of the Natural Intelligence of the user, that decides, the same way, to use or not a feature. So it may demonstrates that Artificial intelligence and Natural Intelligence can cooperate.
In this perspective, one already can speak of Human Bananas.